Непрерывность функции в точке.
Точки разрыва и их классификация.
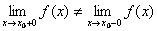
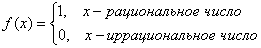
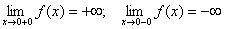 .
.

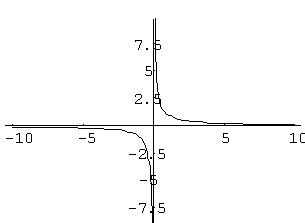
Скачок.
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов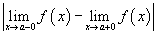 называется скачком функции.
называется скачком функции.
Вертикальные асимптоты.
Если хотя бы один из односторонних пределов f(x0 − 0), f (x0 + 0) равен бесконечности, то прямая x = x 0 называется вертикальной асимптотой графика функции y = f(x).
Вертикальные асимптоты
Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
т.е.
| (1) |
| " O( f(x0) ) $ O(x0) : x О O(x0) Ю f(x) О O( f(x0) ) . |
Точки разрыва и их классификация.
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
не является непрерывной в любой точке х0.
Пример. Функция f(x) = 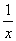 имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
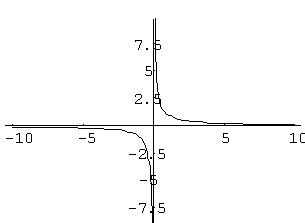
Скачок.
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов
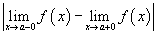 называется скачком функции.
называется скачком функции.Вертикальные асимптоты.
Если хотя бы один из односторонних пределов f(x0 − 0), f (x0 + 0) равен бесконечности, то прямая x = x 0 называется вертикальной асимптотой графика функции y = f(x).
Вертикальные асимптоты
1. Линия задана уравнением y = f(x). Если 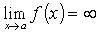 , то x = a - вертикальная асимптота. В частности, если
, то x = a - вертикальная асимптота. В частности, если 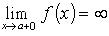 , то x = a - вертикальная правосторонняя асимптота; если же
, то x = a - вертикальная правосторонняя асимптота; если же 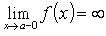 , то x = a - вертикальная левосторонняя асимптота.
, то x = a - вертикальная левосторонняя асимптота.
2. Линия задана уравнениями x = x(t), y = y(t). Если 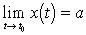 ,
, 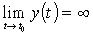 , то x = a - вертикальная асимптота. В частности, если
, то x = a - вертикальная асимптота. В частности, если 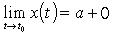 ,
, 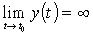 , то x = a - вертикальная правосторонняя асимптота; если же
, то x = a - вертикальная правосторонняя асимптота; если же 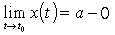 ,
, 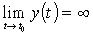 , то x = a - вертикальная левосторонняя асимптота.
, то x = a - вертикальная левосторонняя асимптота.