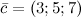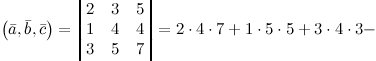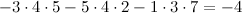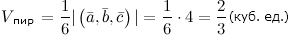Определение смешанного произведения трёх векторов, его свойства и геометрический смысл

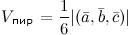
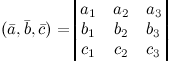
Геометрический смысл смешанного произведения
Геометрический смысл смешанного произведения: если тройка векторов 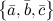 правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 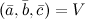 . В случае левой тройки
. В случае левой тройки 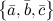 смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:
смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: 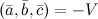 . Если
. Если 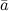 ,
, 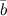 и
и 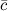 компланарны, то их смешанное произведение равно нулю.
компланарны, то их смешанное произведение равно нулю.
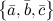 правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 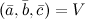 . В случае левой тройки
. В случае левой тройки 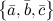 смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:
смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: 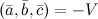 . Если
. Если 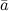 ,
, 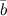 и
и 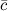 компланарны, то их смешанное произведение равно нулю.
компланарны, то их смешанное произведение равно нулю.
Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах 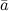 ,
, 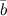 и
и 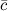 равен модулю смешанного произведения этих векторов:
равен модулю смешанного произведения этих векторов:
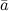 ,
, 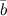 и
и 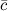 равен модулю смешанного произведения этих векторов:
равен модулю смешанного произведения этих векторов:
Объем пирамиды, построенной на этой тройке векторов равен
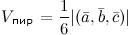
Свойства смешанного произведения:
1° 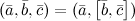
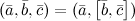
2° 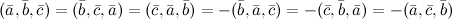
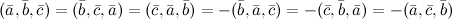
3° Три вектора компланарны тогда и только тогда, когда 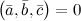
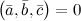
4° Тройка векторов является правой тогда и только тогда, когда 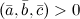 . Если же
. Если же 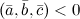 , то векторы
, то векторы 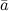 ,
, 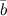 и
и 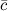 образуют левую тройку векторов.
образуют левую тройку векторов.
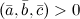 . Если же
. Если же 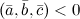 , то векторы
, то векторы 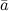 ,
, 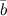 и
и 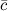 образуют левую тройку векторов.
образуют левую тройку векторов.
5° 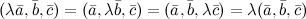
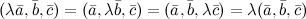
6° 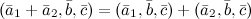
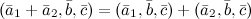
7° 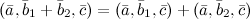
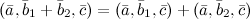
8° 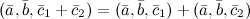
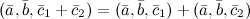
9° 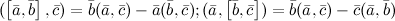
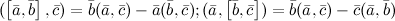
10° Тождество Якоби: 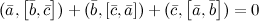
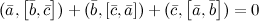
Если векторы 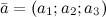 ,
, 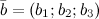 и
и 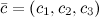 заданы своими координатами, то их смешанное произведение вычисляется по формуле
заданы своими координатами, то их смешанное произведение вычисляется по формуле
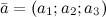 ,
, 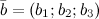 и
и 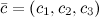 заданы своими координатами, то их смешанное произведение вычисляется по формуле
заданы своими координатами, то их смешанное произведение вычисляется по формуле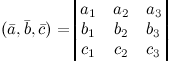
Пример
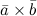 на вектор
на вектор 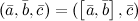
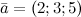 ,
, 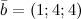 ,
,