Координаты суммы, разности векторов и произведения вектора на число.
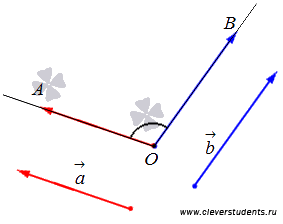
Определение угла между векторами в пространстве.
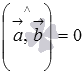когда векторы 
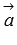и 
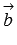сонаправленные, 
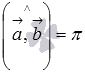когда векторы 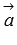и 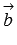противоположно направленные.
Если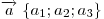 
и 
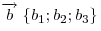— два произвольных вектора, то:
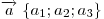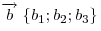и — два произвольных вектора, то:- Координаты суммы векторов равны сумме соответствующих координат слагаемых
.
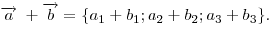- Координаты разности векторов равны разности соответствующих координат этих векторов
- Координаты произведения на число
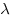равны произведению соответствующих координат векторов на данное число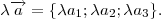
Определение угла между векторами в пространстве.
Определение.
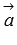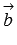Угол между векторами и будем обозначать как 
.
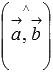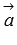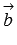и будем обозначать как .
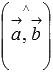Понятно, что угол между векторами может принимать значения от 0 до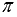 
или, что то же самое, от 
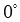до 
.
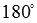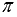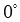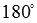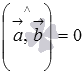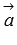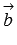или, что то же самое, от до . когда векторы и сонаправленные, 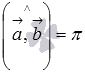когда векторы 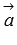и 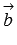противоположно направленные.
Определение.
Векторы 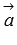и 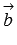называются перпендикулярными, если угол между ними равен 
(
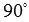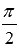радиан).
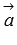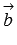и называются перпендикулярными, если угол между ними равен 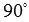( 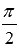радиан).
Если хотя бы один из векторов 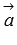и 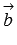нулевой, то угол 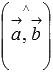не определен.
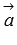и 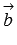нулевой, то угол 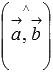не определен.