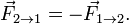Гидродинамика и аэродинамика.
Гидродина́мика и аэродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.
Характеристики течения.
Течение - движение жидкости
Поток жидкости (газа) и уравнение неразрывности.
Поток - совокупность частиц движущейся жидкости.
Уравнения неразрывности для несжимаемой жидкости: произведение скорости течения несжимаемой жидкости на поперечной сечение трубки тока есть величина постоянная для данной трубки тока.
S1v1 = S2v2 или Sv=const. где S-площадь поперечного сечения
Уравнение Бернулли для жидкости (газа).
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
p— плотность жидкости,
v— скорость потока,
h— высота, на которой находится рассматриваемый элемент жидкости,
p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
g— ускорение свободного падения.
Гидравлический пресс.
Гидравлический пресс — это простейшая гидравлическая машина , предназначенная для создания больших сжимающих усилий.
Гидравлический пресс состоит из двух сообщающихся гидравлических цилиндров (с поршнями) разного диаметра. Цилиндр заполняется гидравлической жидкостью, водой, маслом или другой подходящей жидкостью. По законам французского философа и учёного Паскаля, давление (то есть сила, действующая на единицу площади) в любом месте жидкости (или газа), находящейся в покое, одинаково по всем направлениям и одинаково передается по всему объёму. Закон Паскаля — самый главный закон гидростатики. Все заводы гидравлических прессов при их производстве основываются на законе гидростатики. По сути гидравлический пресс можно сравнить с эффектом рычага, где в качестве передающего усилие объекта используется жидкость, а усилие зависит от величины отношения площадей рабочих поверхностей. но это не обязательно
Гидродина́мика и аэродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.
Характеристики течения.
Течение - движение жидкости
Поток жидкости (газа) и уравнение неразрывности.
Поток - совокупность частиц движущейся жидкости.
Уравнения неразрывности для несжимаемой жидкости: произведение скорости течения несжимаемой жидкости на поперечной сечение трубки тока есть величина постоянная для данной трубки тока.
S1v1 = S2v2 или Sv=const. где S-площадь поперечного сечения
Уравнение Бернулли для жидкости (газа).
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
p— плотность жидкости,
v— скорость потока,
h— высота, на которой находится рассматриваемый элемент жидкости,
p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
g— ускорение свободного падения.
Гидравлический пресс.
Гидравлический пресс — это простейшая гидравлическая машина , предназначенная для создания больших сжимающих усилий.
Гидравлический пресс состоит из двух сообщающихся гидравлических цилиндров (с поршнями) разного диаметра. Цилиндр заполняется гидравлической жидкостью, водой, маслом или другой подходящей жидкостью. По законам французского философа и учёного Паскаля, давление (то есть сила, действующая на единицу площади) в любом месте жидкости (или газа), находящейся в покое, одинаково по всем направлениям и одинаково передается по всему объёму. Закон Паскаля — самый главный закон гидростатики. Все заводы гидравлических прессов при их производстве основываются на законе гидростатики. По сути гидравлический пресс можно сравнить с эффектом рычага, где в качестве передающего усилие объекта используется жидкость, а усилие зависит от величины отношения площадей рабочих поверхностей. но это не обязательно

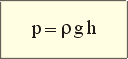


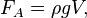













 ;
;  ;
;