Определение предела функции в точке по Гейне и по Коши.
ПРИМЕР
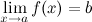 Смотреть решение...
Смотреть решение...
Геометрическая интерпретация предела.
Геометрическая интерпретация определения по Коши. Т.к. неравенство (1) равносильно: то какова бы ни была полоса, ограниченная прямыми
то какова бы ни была полоса, ограниченная прямыми  и
и  , найдется интервал
, найдется интервал  , такой что все точки графика
, такой что все точки графика  с абсциссами из этого интервала (кроме быть может точки с абсциссами
с абсциссами из этого интервала (кроме быть может точки с абсциссами  ) окажутся внутри данной полосы
) окажутся внутри данной полосы
Единственность предела.
Теорема. Последовательность может иметь только один предел.
Предел функции по Гейне
Значение  называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 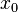 , если для любой последовательности точек
, если для любой последовательности точек 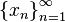 , сходящейся к
, сходящейся к 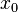 , но не содержащей
, но не содержащей 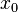 в качестве одного из своих элементов (то есть в проколотой окрестности
в качестве одного из своих элементов (то есть в проколотой окрестности 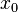 ), последовательность значений функции
), последовательность значений функции  сходится к
сходится к  .
.
 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 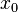 , если для любой последовательности точек
, если для любой последовательности точек 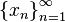 , сходящейся к
, сходящейся к 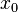 , но не содержащей
, но не содержащей 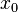 в качестве одного из своих элементов (то есть в проколотой окрестности
в качестве одного из своих элементов (то есть в проколотой окрестности 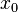 ), последовательность значений функции
), последовательность значений функции  сходится к
сходится к  .
.Предел функции по Коши
Значение  называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 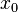 , если для любого наперёд взятого положительного числа
, если для любого наперёд взятого положительного числа  найдётся отвечающее ему положительное число
найдётся отвечающее ему положительное число 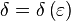 такое, что для всех аргументов
такое, что для всех аргументов  , удовлетворяющих условию
, удовлетворяющих условию 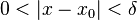 , выполняется неравенство
, выполняется неравенство  .
.
 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 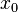 , если для любого наперёд взятого положительного числа
, если для любого наперёд взятого положительного числа  найдётся отвечающее ему положительное число
найдётся отвечающее ему положительное число 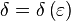 такое, что для всех аргументов
такое, что для всех аргументов  , удовлетворяющих условию
, удовлетворяющих условию 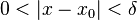 , выполняется неравенство
, выполняется неравенство  .
.ПРИМЕР
ЗАДАЧА 433 Сформулировать при помощи неравенств
Сформулировать при помощи неравенств следующее утверждение: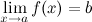 Смотреть решение...
Смотреть решение...Геометрическая интерпретация предела.
Геометрическая интерпретация определения по Коши. Т.к. неравенство (1) равносильно:
Единственность предела.
Теорема. Последовательность может иметь только один предел.

