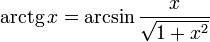Обратные тригонометрические функции, их свойства и графики.
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.
Функция arcsin
Арксинусом числа m называется такое значение угла x, для которого 

Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 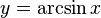 является строго возрастающей.
является строго возрастающей.
 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 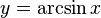 является строго возрастающей.
является строго возрастающей. при
при 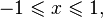
 при
при 
![D(\arcsin x)=[-1; 1]\qquad](http://upload.wikimedia.org/math/6/3/2/6325ff9dcc6bc9be23bcd886c4dc179c.png) (область определения),
(область определения),![E(\arcsin x) = \left[-\frac{\pi}{2}; \frac{\pi}{2}\right]\qquad](http://upload.wikimedia.org/math/4/9/8/4986c64f5129adab13f65a88c3d9eda8.png) (область значений).
(область значений).
[править]Свойства функции arcsin
 (функция является нечётной).
(функция является нечётной).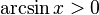 при
при  .
. при
при 
 при
при 



[править]Получение функции arcsin
Дана функция  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 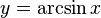 функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений —
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](http://upload.wikimedia.org/math/5/c/d/5cd520b8b7a376ccf94eb254281f0eb8.png) . Так как для функции
. Так как для функции  на интервале
на интервале ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](http://upload.wikimedia.org/math/5/c/d/5cd520b8b7a376ccf94eb254281f0eb8.png) каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция
каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция  график которой симметричен графику функции
график которой симметричен графику функции  на отрезке
на отрезке ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](http://upload.wikimedia.org/math/5/c/d/5cd520b8b7a376ccf94eb254281f0eb8.png) относительно прямой
относительно прямой 
 На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 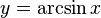 функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений —
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](http://upload.wikimedia.org/math/5/c/d/5cd520b8b7a376ccf94eb254281f0eb8.png) . Так как для функции
. Так как для функции  на интервале
на интервале ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](http://upload.wikimedia.org/math/5/c/d/5cd520b8b7a376ccf94eb254281f0eb8.png) каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция
каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция  график которой симметричен графику функции
график которой симметричен графику функции  на отрезке
на отрезке ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](http://upload.wikimedia.org/math/5/c/d/5cd520b8b7a376ccf94eb254281f0eb8.png) относительно прямой
относительно прямой 
[править]Функция arccos
Арккосинусом числа m называется такое значение угла x, для которого 

Функция 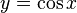 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 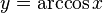 является строго убывающей.
является строго убывающей.
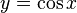 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 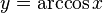 является строго убывающей.
является строго убывающей. при
при 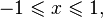
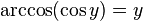 при
при 
![D(\arccos x)=[-1; 1],](http://upload.wikimedia.org/math/e/6/2/e62e5846d71c12654c0c1a3b66c603ab.png) (область определения),
(область определения),![E(\arccos x)=[0; \pi].](http://upload.wikimedia.org/math/7/6/2/7625fee35d41ee040526655645c532d0.png) (область значений).
(область значений).
[править]Свойства функции arccos
 (функция центрально-симметрична относительно точки
(функция центрально-симметрична относительно точки  ), является индифферентной.
), является индифферентной. при
при 
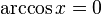 при
при 
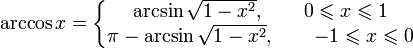
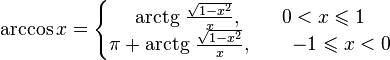



[править]Получение функции arccos
Дана функция 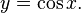 На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 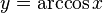 функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения —
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — ![[0; \pi].](http://upload.wikimedia.org/math/0/8/2/0824d29d730954716bd9aaa8e2284490.png) На этом отрезке
На этом отрезке 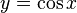 строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке
строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке ![[0; \pi]](http://upload.wikimedia.org/math/1/6/6/166583a10d3b16bca60d1e784651c2fd.png) существует обратная функция
существует обратная функция  график которой симметричен графику
график которой симметричен графику 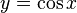 на отрезке
на отрезке ![[0; \pi]](http://upload.wikimedia.org/math/1/6/6/166583a10d3b16bca60d1e784651c2fd.png) относительно прямой
относительно прямой 
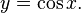 На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 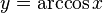 функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения —
функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — ![[0; \pi].](http://upload.wikimedia.org/math/0/8/2/0824d29d730954716bd9aaa8e2284490.png) На этом отрезке
На этом отрезке 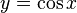 строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке
строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке ![[0; \pi]](http://upload.wikimedia.org/math/1/6/6/166583a10d3b16bca60d1e784651c2fd.png) существует обратная функция
существует обратная функция  график которой симметричен графику
график которой симметричен графику 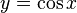 на отрезке
на отрезке ![[0; \pi]](http://upload.wikimedia.org/math/1/6/6/166583a10d3b16bca60d1e784651c2fd.png) относительно прямой
относительно прямой 
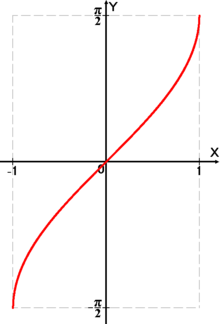
[править]Функция arctg
Арктангенсом числа m называется такое значение угла  , для которого
, для которого 
 , для которого
, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго возрастающей.
является строго возрастающей.
 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго возрастающей.
является строго возрастающей. при
при 
 при
при 


[править]Свойства функции arctg
 , при x > 0.
, при x > 0.
 , при x > 0.
, при x > 0.
[править]Получение функции arctg
Дана функция  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие  функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —
функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —  На этом отрезке
На этом отрезке  строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале
строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале  существует обратная
существует обратная  , график которой симметричен графику
, график которой симметричен графику  на отрезке
на отрезке  относительно прямой
относительно прямой 
 На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие  функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —
функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —  На этом отрезке
На этом отрезке  строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале
строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале  существует обратная
существует обратная  , график которой симметричен графику
, график которой симметричен графику  на отрезке
на отрезке  относительно прямой
относительно прямой 
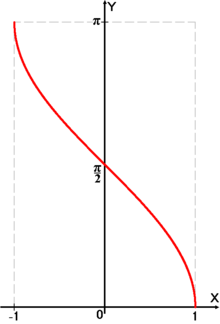
[править]Функция arcctg
Арккотангенсом числа m называется такое значение угла x, для которого 

Функция  непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго убывающей.
является строго убывающей.
 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция  является строго убывающей.
является строго убывающей. при
при 
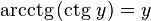 при
при 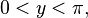


[править]Свойства функции arcctg
 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 
 при любых
при любых 
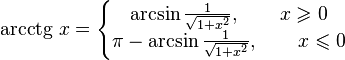
[править]Получение функции arcctg
Дана функция  . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие  функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз —
функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз —  . На этом отрезке
. На этом отрезке  строго убывает и принимает все свои значения только один раз, следовательно, на интервале
строго убывает и принимает все свои значения только один раз, следовательно, на интервале  существует обратная функция
существует обратная функция  , график которой симметричен графику
, график которой симметричен графику  на отрезке
на отрезке  относительно прямой
относительно прямой  График симметричен к арктангенсу
График симметричен к арктангенсу
 . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие  функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз —
функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз —  . На этом отрезке
. На этом отрезке  строго убывает и принимает все свои значения только один раз, следовательно, на интервале
строго убывает и принимает все свои значения только один раз, следовательно, на интервале  существует обратная функция
существует обратная функция  , график которой симметричен графику
, график которой симметричен графику  на отрезке
на отрезке  относительно прямой
относительно прямой  График симметричен к арктангенсу
График симметричен к арктангенсу