[Зачет 71] Определение скалярного произведения векторов. Вывод формулы для вычисления скалярного произведения векторов, заданных своими координатами в ортонормированном базисе. Вычисление косинуса угла между ненулевыми векторами и прямыми. Условие перпендикулярности векторов.

Определение скалярного произведения векторов.

Определение. Скалярным произведением двух ненулевых векторов называется произведение модулей этих векторов на косинус угла между ними. Если из двух данных векторов хотя бы один нулевой, то скалярное произведение двух таких векторов считается равным нулю.

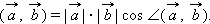Определение. (в координатах) Скалярным произведение двух векторов, заданных своими координатами, равно сумме произведений одноименных координат этих векторов.

вектор А* вектор Б = x1x2+y1y2+z1z2

Вывод формулы для вычисления скалярного произведения векторов, заданных своими координатами в ортонормированном базисе. Вычисление косинуса угла между ненулевыми векторами и прямыми. Условие перпендикулярности векторов.