ФизМат: [Зачет 60] Основные способы раскрытия неопределённостей. Примеры.

четверг, 16 мая 2013 г.

[Зачет 60] Основные способы раскрытия неопределённостей. Примеры.

Основные способы раскрытия неопределённостей. Примеры.

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

$(\infty-\infty)$

$\left (\frac{\infty}{\infty} \right )$

$\left (\frac{0}{0} \right )$

$\left (~0^0 \right )$

$\left (1^\infty \right )$

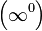$\left (\infty^0 \right )$

$(0\cdot\infty)$

(Здесь $~0$ - бесконечно малая величина, а $\infty$ - бесконечно большая величина)

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Теорема Лопиталя:

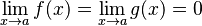$\lim_{x\to a}{f(x)}=\lim_{x\to a}{g(x)}=0$ либо $\infty$ ;
$~f(x)$ и $~g(x)$ дифференцируемы в проколотой окрестности $~a$ ;
$g'(x)\neq 0$ в проколотой окрестности $~a$ ;
существует $\lim_{x\to a}{\frac{f'(x)}{g'(x)}}$ ,

тогда существует $\lim_{x\to a}{\frac{f(x)}{g(x)}} = \lim_{x\to a}{\frac{f'(x)}{g'(x)}}$ .

Пределы также могут быть односторонними.