Электрическая емкость проводника.
Конденсатор. Емкость плоского конденсатора.
Соединение конденсаторов.
Энергия, накопленная в конденсаторе.
Как известно из механики F=mg, аналогично в электрике F=qE, роль массы играет заряд, а роль сили притяжения напряжённость поля.
C другой же стороны работа также равна разнице потенциальных энергий A=W1-W2=W.
Таким образом используя эти два выражения можно сделать вывод что потенциальная энергия накопленная в конденсаторе равна:
Если провести аналогию с механикой: Представим камень, находящийся на крыше здания. Здесь взаимодействует масса земли с массой камня посредством силы тяжести, а здание высотой hпротиводействует силе гравитации. Если здание убрать камень упадет, следовательно, потенциальная энергия перейдет в кинетическую.
В электростатике же есть два разноименных заряда стремящихся притянутся друг к другу им противодействует диэлектрик толщиной d находящийся между обкладками . Если обкладки замкнуть между собой то потенциальная энергия заряда перейдет в кинетическую то есть в тепло.
В электротехнике формула для энергии в таком виде не применяется. Ее удобно выразить через емкость конденсатора и напряжение, до которого он заряжен.
Так как заряд конденсатора определяется зарядом одной из его пластин то напряжённость поля, создаваемая ею, будет равна E/2. Поскольку общее поле складывается из полей создаваемых обеими обкладками заряжении одинаково, но с противоположным знаком.
Следовательно, энергия конденсатора будет иметь вид: W=q(E/2)d
Поскольку напряжение можно выразить через напряжённость и расстояние(U=Ed) подставим его в нашу формулу получим: W=qU/2
А теперь используя выражение для емкости, C=q/U получим окончательный результат.

Энергия электрического поля.
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
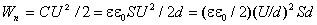 Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
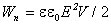 Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна
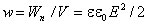 C учетом соотношения
C учетом соотношения 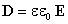 можно записать
можно записать
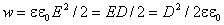 В изотропном диэлектрике направления векторов D и E совпадают и
В изотропном диэлектрике направления векторов D и E совпадают и 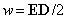
Подставим выражение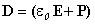 , получим
, получим
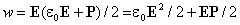 Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов qi на величину dri, составляет
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов qi на величину dri, составляет
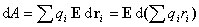 Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно,
Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно, 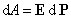 .
.
Вектор P связан с вектором E соотношением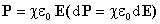 . Подставив это выражение в формулу для работы, получим
. Подставив это выражение в формулу для работы, получим
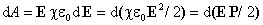 Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика
Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика
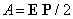 .
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:
.
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:
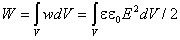
Плотность энергии электрического поля.
Объемная плотность энергии электрического поля называют физическую
величину равную отношению потенциальной энергии поля, заключенной в элементе
объема, к этому объему
объемная плотность энергии электрического поля равна
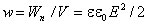
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
В Международной системе единиц (СИ) ёмкость измеряется в фарадах.
Конденсатор. Емкость плоского конденсатора.
Соединение конденсаторов.
Параллельное соединение конденсаторов
| |
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора
| |
 |  |
Вывод: При параллельном соединении конденсаторов
а) заряды складываются,
б) напряжения одинаковые,
в) емкости складываются.
Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов
|  |
Последовательное соединение конденсаторов
| |
Производят только одно соединение, а две оставшиеся обкладки - одна от конденсатора С1 другая от конденсатора С2 - играют роль обкладок нового конденсатора.
| |
 |  |
Вывод: При последовательном соединении конденсаторов
а) напряжения складываются,
б) заряды одинаковы,
в) складываются величины, обратные емкости.
Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов.
|  |
Энергия, накопленная в конденсаторе.
При заряде конденсатора внешний источник расходует энергию на разделение зарядов на положительные и отрицательные. Которые будут находиться на обкладках конденсатора. Следовательно, исходя из закона сохранения энергии, она никуда не пропадает, а остается в конденсаторе. Энергия в конденсаторе запасается в виде силы взаимодействия положительных и отрицательных зарядов находящихся на его обкладках. То есть в виде электрического поля. Которое сосредоточено между пластинами. Это взаимодействие стремится притянуть одну обкладку к другой, поскольку, как известно разноименные заряды притягиваются.
Как известно из механики F=mg, аналогично в электрике F=qE, роль массы играет заряд, а роль сили притяжения напряжённость поля.
Работа по перемещению заряда в электрическом поле выглядит так:A=qEd1-qEd2=qEd
C другой же стороны работа также равна разнице потенциальных энергий A=W1-W2=W.
Таким образом используя эти два выражения можно сделать вывод что потенциальная энергия накопленная в конденсаторе равна:
W=qEd
Формула 1 — Энергия заряженного конденсатора
Не трудно заметить, что формула очень похожа на потенциальную энергию из механики W=mgh.
Если провести аналогию с механикой: Представим камень, находящийся на крыше здания. Здесь взаимодействует масса земли с массой камня посредством силы тяжести, а здание высотой hпротиводействует силе гравитации. Если здание убрать камень упадет, следовательно, потенциальная энергия перейдет в кинетическую.
В электростатике же есть два разноименных заряда стремящихся притянутся друг к другу им противодействует диэлектрик толщиной d находящийся между обкладками . Если обкладки замкнуть между собой то потенциальная энергия заряда перейдет в кинетическую то есть в тепло.
В электротехнике формула для энергии в таком виде не применяется. Ее удобно выразить через емкость конденсатора и напряжение, до которого он заряжен.
Так как заряд конденсатора определяется зарядом одной из его пластин то напряжённость поля, создаваемая ею, будет равна E/2. Поскольку общее поле складывается из полей создаваемых обеими обкладками заряжении одинаково, но с противоположным знаком.
Следовательно, энергия конденсатора будет иметь вид: W=q(E/2)d
Поскольку напряжение можно выразить через напряжённость и расстояние(U=Ed) подставим его в нашу формулу получим: W=qU/2
А теперь используя выражение для емкости, C=q/U получим окончательный результат.
Энергия заряженного конденсатора имеет вид:

Энергия электрического поля.
Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Подставим выражение
Вектор P связан с вектором E соотношением
Плотность энергии электрического поля.
Объемная плотность энергии электрического поля называют физическую
величину равную отношению потенциальной энергии поля, заключенной в элементе
объема, к этому объему
объемная плотность энергии электрического поля равна
 где
где  —
—  — потенциал проводника.
— потенциал проводника.
