[Зачет 66] Определение линейно зависимой и линейно независимой системы векторов. Доказательство свойств системы линейно зависимых векторов.

Определение линейно зависимой и линейно независимой системы векторов.

   Линейная зависимость и независимость векторов 

     Система 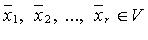 линейно зависима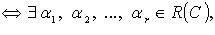 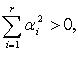  что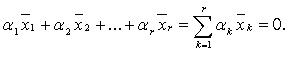 

 Система 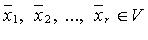 линейно независима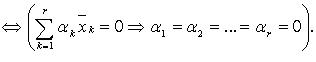 

Доказательство свойств системы линейно зависимых векторов.

Доказательства.

1. Любая система векторов e₁,e₂, ..., e_k линейного пространства, содержащая нулевой вектор, линейн зависима.

2. Любая система векторов e₁,e₂, ..., e_k линейного пространства, содержащая пару взаимно противоположных векторов, линейн зависима.

3. Любая подсистема векторов линейно независимой системы векторов линейного пространства линейно независима.

4. Любая система векторов линейного пространства, содержащая линейно зависимую подсистему векторов, линейно зависима.

5. Система векторов линейного пространства линейно зависма тогда и только тогда, когда хотя бы один из векторов системы линейно выражается через остальные векторы системы (представлен в виде разложения по векторам системы).

6. Система векторов линейного пространства линейно независма любая её подсистемы векторов.

6. Система векторов, состоящая из одного ненулевого вектора линейного прострранства, линейно независима.