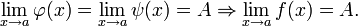Теоремы о предельном переходе в неравенствах.
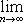
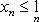
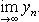
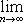
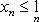
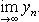
Теорема о зажатой функции.
Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер Nтакой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b -a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
Замечание. Элементы сходящейся последовательности {xn} могут удовлетворять строгому неравенству xn > b, однако при этом предел a может оказаться равным b. Например, если 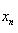
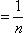 , то xn > 0, однако
, то xn > 0, однако 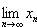
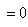 .
.
Следствие 1. Если элементы xn и yn сходящихся последовательностей {xn} и {yn}, начиная с некоторого номера, удовлетворяют неравенству xn≤ yn, то их пределы удовлетворяют такому же неравенству:
В самом деле, элементы последовательности {yn - xn} неотрицательны, а поэтому неотрицателен и ее предел 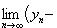
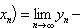
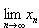 . Отсюда следует, что
. Отсюда следует, что
Следствие 2. Если все элементы сходящейся последовательности {xn} находятся на сегменте [a, b], то и ее предел c также находится на этом сегменте.
В самом деле, так как a ≤ xn ≤ b, то a ≤ c ≤ b.
Следующая теорема играет важную роль в различных приложениях.
Теорема. Пусть {xn} и {zn} - сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {yn} удовлетворяют неравенствам xn ≤ yn ≤ zn. Тогда последовательность {yn} сходится и имеет предел a.
Доказательство. Нам достаточно доказать, что последовательность {yn - a} является бесконечно малой. Обозначим через N* номер, начиная с которого выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполняться также неравенства xn - a≤ yn - a ≤ zn - a. Отсюда следует, что при n ≥ N* элементы последовательности {yn - a} удовлетворяют неравенству
|yn - a| ≤ max {|xn - a|, |zn - a|}.
Так как 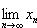
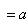 и
и 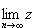
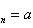 , то для любого ε > 0 можно указать номера N1 и N2 такие, что при n ≥ N1 |xn - a| < ε, а при n ≥ N2 |zn - a| < ε. Пусть N= max{N*, N1, N2}. Начиная с этого номера, имеет место неравенство |yn - a| < ε. Итак, последовательность {yn - a} - бесконечно малая. Теорема доказана.
, то для любого ε > 0 можно указать номера N1 и N2 такие, что при n ≥ N1 |xn - a| < ε, а при n ≥ N2 |zn - a| < ε. Пусть N= max{N*, N1, N2}. Начиная с этого номера, имеет место неравенство |yn - a| < ε. Итак, последовательность {yn - a} - бесконечно малая. Теорема доказана.
Теорема о зажатой функции.
Если функция  такая, что
такая, что 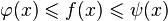 для всех
для всех  в некоторой окрестности точки
в некоторой окрестности точки  , причем функции
, причем функции  и
и 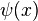 имеют одинаковый предел при
имеют одинаковый предел при  , то существует предел функции
, то существует предел функции  при
при  , равный этому же значению, то есть
, равный этому же значению, то есть
 такая, что
такая, что 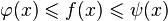 для всех
для всех  в некоторой окрестности точки
в некоторой окрестности точки  , причем функции
, причем функции  и
и 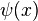 имеют одинаковый предел при
имеют одинаковый предел при  , то существует предел функции
, то существует предел функции  при
при  , равный этому же значению, то есть
, равный этому же значению, то есть