[Зачет 70] Определение ортонормированного базиса и прямоугольной декартовой системы координат (ПДСК). Вывод формул для вычисления длины вектора, заданного своими координатами в ортонормированном базисе, расстояния между двумя точками.

Определение ортонормированного базиса и прямоугольной декартовой системы координат (ПДСК). 

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

Вывод формул для вычисления длины вектора, заданного своими координатами в ортонормированном базисе, расстояния между двумя точками. 

Нахождение длины вектора по координатам.

Длину вектора  будем обозначать . Аналогичное обозначение имеет модуль числа, и длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор  и он имеет координаты . Получим формулу, позволяющую находить длину вектора  через координаты  и .

Отложим от начала координат (от точки О) вектор . Обозначим проекции точки А на координатные оси как  и  соответственно и рассмотрим прямоугольник  с диагональю ОА.

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что  и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора  по его координатам на плоскости имеет вид .

Если вектор  представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты  и  являются координатами вектора  в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

.

Теперь получим формулу для нахождения длины вектора  по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор  и обозначим проекции точки А на координатные оси как  и . Тогда мы можем построить на сторонах  и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае  (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора  в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле .

Пример.

Вычислите длину вектора , где  - орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора  по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Ответ:

.

Длина вектора через координаты точек его начала и конца.

А как найти длину вектора, если даны координаты точек его начала и конца?

В предыдущем пункте мы получили формулы для нахождения длины вектора по его координатам на плоскости и в трехмерном пространстве. Тогда мы можем ими воспользоваться, если найдем координаты вектора по координатам точек его начала и конца.

Таким образом, если на плоскости заданы точки  и , то вектор  имеет координаты  и его длина вычисляется по формуле , а формула для нахождения длины вектора  по координатам точек  и  трехмерного пространства имеет вид .

Рассмотрим решения примеров.

Пример.

Найдите длину вектора , если в прямоугольной декартовой системе координат .

Решение.

Можно сразу применить формулу для нахождения длины вектора по координатам точек начала и конца на плоскости :

Вторым вариантом решения является определение координат вектора через координаты точек и применение формулы :

Ответ:

.

Пример.

Определите, при каких значениях  длина вектора  равна , если .

Решение.

Длина вектора  по координатам точек начала и конца может быть найдена как

Приравняв полученное значение длины вектора к , вычислим искомые :

Ответ:

при .

Нахождение длины вектора по теореме косинусов.

Большинство задач на нахождение длины вектора решаются в координатах. Однако, когда координаты вектора не известны приходится искать другие пути решения.

Пусть известны длины двух векторов ,  и угол между ними (или косинус угла), а требуется найти длину вектора  или . В этом случае можно по теореме косинусов в треугольнике АВС вычислить длину стороны ВС, которая равна искомой длине вектора.

Разберем решение примера для пояснения сказанного.

Пример.

Длины векторов  и  равны 3 и 7 соответственно, а угол между ними равен . Вычислите длину вектора .

Решение.

Длина вектора  равна длине стороны ВС в треугольнике АВС. Из условия нам известны длины сторон АВ и АС этого треугольника (они равны длинам соответствующих векторов), а также угол между ними, поэтому нам достаточно данных для применения теоремы косинусов:

Таким образом, .

Ответ:

.

Итак, для нахождения длины вектора по координатам используем формулы
 или ,
по координатам точек начала и конца вектора -
 или ,
в некоторых случаях к результату приводит теорема косинусов.

Расстояние между двумя точкамиA1(x1;y1) и A2(x2;y2) в прямоугольной системе координат выражается формулой: 1. d= (x2−x1)2+(y2−y1)2 Порядок точек не играет роли. Расстояние считается положительным. поэтому корень берется с одним знаком (плюс).

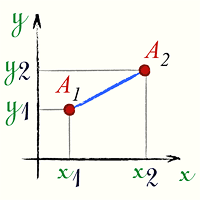Расстояние между двумя точками