четверг, 16 мая 2013 г.

[Зачет 58] Понятие односторонних пределов, необходимое и достаточное условие существования предела функции в точке.

Понятие односторонних пределов, необходимое и достаточное условие существования предела функции в точке. 

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Односторонний предел по Гейне 

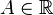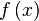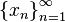  • Число A \in \R называется правосторонним пределом (правым пределом, пределом справа) функции ~f \left( x \right) в точке ~a, если для всякой последовательности \left\{ x_n \right\}_{n = 1}^{\infty}, состоящей из точек, больших числа ~a, которая сама сходится к числу ~a, соответствующая последовательность значений функции \left\{ f \left( x_n \right) \right\}_{n = 1}^{\infty} сходится к числу ~A.
    \lim_{x \to a+} f \left( x \right) = A \Leftrightarrow \forall \left\{ x_n \right\}_{n = 1}^{\infty} \colon \left( \forall k \in \N \colon x_k > a \right) \land \lim_{n \to \infty} x_n = a \Rightarrow \lim_{n \to \infty} \left\{ f \left( x_n \right) \right\}_{n = 1}^{\infty} = A
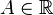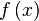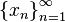  • Число A \in \R называется левосторонним пределом (левым пределом, пределом слева) функции ~f \left( x \right) в точке ~a, если для всякой последовательности \left\{ x_n \right\}_{n = 1}^{\infty}, состоящей из точек, меньших числа ~a, которая сама сходится к числу ~a, соответствующая последовательность значений функции \left\{ f \left( x_n \right) \right\}_{n = 1}^{\infty} сходится к числу ~A.
    \lim_{x \to a-} f \left( x \right) = A \Leftrightarrow \forall \left\{ x_n \right\}_{n = 1}^{\infty} \colon \left( \forall k \in \N \colon x_k < a \right) \land \lim_{n \to \infty} x_n = a \Rightarrow \lim_{n \to \infty} \left\{ f \left( x_n \right) \right\}_{n = 1}^{\infty} = A

Односторонний предел по Коши

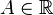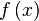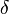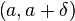  • Число A \in \R называется правосторонним пределом (правым пределом, пределом справа) функции ~f \left( x \right) в точке ~a, если для всякого положительного числа ~\varepsilon отыщется отвечающее ему положительное число ~\delta такое, что для всех точек ~x из интервала \left( a, a + \delta \right) справедливо неравенство \left| f \left( x \right) - A \right| < \varepsilon.
    \lim_{x \to a+} f \left( x \right) = A \Leftrightarrow \forall \varepsilon > 0 ~ \exists \delta = \delta \left( \varepsilon \right) > 0 ~ \forall x \in \left( a, a + \delta \right) \colon \left| f \left( x \right) - A \right| < \varepsilon
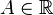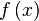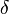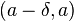  • Число A \in \R называется левосторонним пределом (левым пределом, пределом слева) функции ~f \left( x \right) в точке ~a, если для всякого положительного числа ~\varepsilon отыщется отвечающее ему положительное число ~\delta, такое, что для всех точек ~x из интервала \left( a - \delta, a \right) справедливо неравенство \left| f \left( x \right) - A \right| < \varepsilon.
    \lim_{x \to a-} f \left( x \right) = A \Leftrightarrow \forall \varepsilon > 0 ~ \exists \delta = \delta \left( \varepsilon \right) > 0 ~ \forall x \in \left( a - \delta, a \right) \colon \left| f \left( x \right) - A \right| < \varepsilon


Теорема 2. (Необходимое и достаточное условия существования предела функции в точке.)
Пусть функция f(x) определена в некоторой окрестности точки x0.
         Для того чтобы функция f(x) имела в точки x0 предел необходимо и достаточно, чтобы функция f(x) в некоторой окрестности точки  x0  была представима в виде
                                      f(x)=A+a(x),

где   a(x) – бесконечно малая функция,  А – число.

Доказательство


ЗАДАЧА 390 Задана функция y=f(x) различными

Задана функция y=f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж. Смотреть решение...
Автор: на
Ярлыки: