Числовые функции, их свойства (монотонность, ограниченность, чётность, периодичность).
Определение. Пусть X - числовое множество. Правило сопоставляющее каждому числу x из X некоторое число y, называется числовой функцией, заданной на X.
Если для любых двух значений аргумента x1 и x2 из условия x2 > x1 следует f ( x2 ) > f ( x1 ), то функция f ( x ) называется возрастающей; если для любых x1 и x2 из условия x2 > x1 следует f ( x2 ) < f ( x1 ), то функция f ( x ) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)|
M для всех значений x . Если такого числа не существует, то функция - неограниченная.
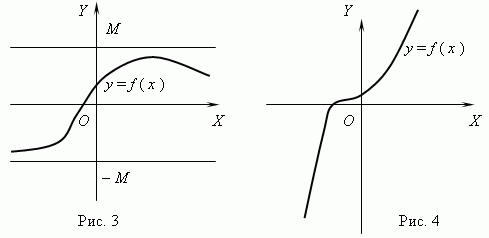Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная.
M для всех значений x . Если такого числа не существует, то функция - неограниченная.
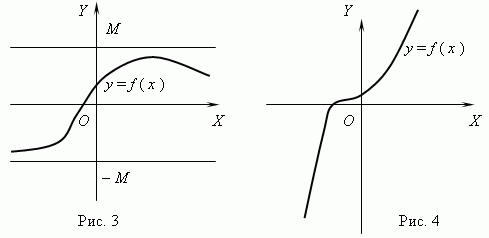Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная.
Если для любого x из области определения функции имеет место: f ( - x ) = f ( x ), то функция называется чётной; если же имеет место: f ( - x ) = - f ( x ), то функция называется нечётной. График чётной функции симетричен относительно оси Y ( рис.5 ), a график нечётной функции симметричен относительно начала координат ( рис.6 ).
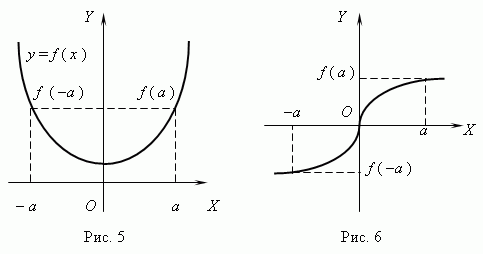
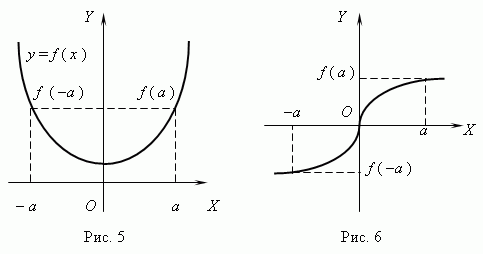
Периодическая функция. Функция f ( x ) - периодическая, если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
П р и м е р 1 . Доказать, что sin x имеет период 2 .
Р е ш е н и е . Мы знаем, что sin ( x+ 2n ) = sin x, где n = 0, ± 1, ± 2, … Следовательно, добавление 2n к аргументу синуса не меняет его значениe. Существует ли другое число с таким же свойством ? Предположим, что P – такое число, т.e. равенство:
sin ( x+ P ) = sin x,
справедливо для любого значения x. Но тогда оно имеет место и при x = / 2 , т.e.
sin ( / 2 + P ) = sin / 2 = 1.
Но по формуле приведения sin ( / 2 + P ) = cos P. Тогда из двух последних равенств следует, что cos P = 1, но мы знаем, что это верно лишь при P = 2n. Так как наименьшим отличным от нуля числом из 2n является 2, то это число и есть период sin x. Аналогично доказывается, что 2 является периодом и для cos x . Докажите, что функции tan x и cot x имеют период .
П р и м е р 2. Какое число является периодом функции sin 2x ?
Р е ш е н и е . Рассмотрим sin 2x = sin ( 2x + 2n ) = sin [ 2 ( x + n ) ] .
Мы видим, что добавление n к аргументу x, не меняет значение функции. Наименьшее отличное от нуля число из n есть , таким образом, это период sin 2x .
П р и м е р 1 . Доказать, что sin x имеет период 2 .
Р е ш е н и е . Мы знаем, что sin ( x+ 2n ) = sin x, где n = 0, ± 1, ± 2, … Следовательно, добавление 2n к аргументу синуса не меняет его значениe. Существует ли другое число с таким же свойством ? Предположим, что P – такое число, т.e. равенство:
sin ( x+ P ) = sin x,
справедливо для любого значения x. Но тогда оно имеет место и при x = / 2 , т.e.
sin ( / 2 + P ) = sin / 2 = 1.
Но по формуле приведения sin ( / 2 + P ) = cos P. Тогда из двух последних равенств следует, что cos P = 1, но мы знаем, что это верно лишь при P = 2n. Так как наименьшим отличным от нуля числом из 2n является 2, то это число и есть период sin x. Аналогично доказывается, что 2 является периодом и для cos x . Докажите, что функции tan x и cot x имеют период .
П р и м е р 2. Какое число является периодом функции sin 2x ?
Р е ш е н и е . Рассмотрим sin 2x = sin ( 2x + 2n ) = sin [ 2 ( x + n ) ] .
Мы видим, что добавление n к аргументу x, не меняет значение функции. Наименьшее отличное от нуля число из n есть , таким образом, это период sin 2x .
Соответствие, относящее к каждому у0E(f) единственное x0D(f), называется обратной функцией x=f-1(y) по отношению к функции y=f(x).
