Многочлен как функция и его график.
Где n - любое натуральное число или 0, а a0, a1, ..., an - какие-то действительные числа, называемые коэффициентами многочлена.
Утверждение. Любая непрерывная кривая, имеющая на некотором промежутке a ≤ x ≤ b
с каждой из прямых, параллельных Oy, в точности одну общую точку, может быть приближенно задана как график функции y= Pn(x), где Pn(x) — многочлен.
Обобщённая теорема Виета.
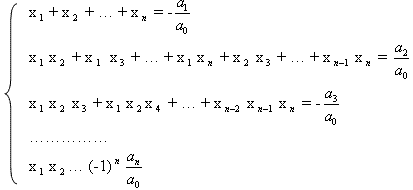
Пример:





Определение. Функция f(x) действительной или комплексной переменной x называется многочленом, если она может быть представлена в виде:
f(x)=a0xn+a1xn-1+a2xn-2+...+an-2x2+an-1x+an
Утверждение. Любая непрерывная кривая, имеющая на некотором промежутке a ≤ x ≤ b
с каждой из прямых, параллельных Oy, в точности одну общую точку, может быть приближенно задана как график функции y= Pn(x), где Pn(x) — многочлен.
Обобщённая теорема Виета.
Пусть х1; х2… хn – корни многочлена
Р(х) = a0xn + a1xn-1 + an-1x + an
тогда
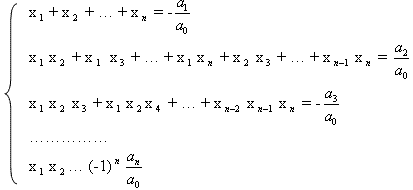
- рациональные корни многочлена
Р(х) = a0xn + a1xn-1 + an-1x + an с целыми коэффициентами имеют вид x = 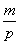 , где m – делитель свободного члена an, p – делитель старшего коэффициента a0
, где m – делитель свободного члена an, p – делитель старшего коэффициента a0
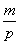 , где m – делитель свободного члена an, p – делитель старшего коэффициента a0
, где m – делитель свободного члена an, p – делитель старшего коэффициента a0
- приведенный многочлен с целыми коэффициентами (a0 = 1) не может иметь дробных корней. Целые корни такого многочлена являются делителями его свободного члена.
Пример:




