[Билет 18] Определение синуса, косинуса, тангенса и котангенса действительного числа. Свойства и графики тригонометрических функций.

Определение синуса, косинуса, тангенса и котангенса действительного числа.

Определение. Число, равное ординате точки М единичной окружности, называется синусом угла α

Определение. Число равное абсциссе точки М единичной окружности, называется косинусом угла α.

Определение. Отношение ординаты точки М к ее абсциссе называется тангенсом угла α.

Определение.  Отношение абсциссы к ординате - котангенсом угла α

Свойства и графики тригонометрических функций.

Функция синус

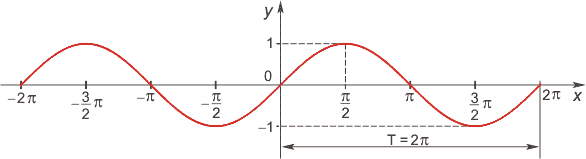Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2π: sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R. sin x = 0 при x = π·k, k ∈ Z. sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z. sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z. Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках: Наибольшее значение функции sin x = 1 в точках: Наименьшее значение функции sin x = −1 в точках:

---

Функция косинус

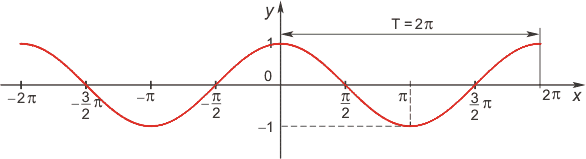Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом 2π: cos(x+2π·k) = cos x, где k ∈ Z для всех х ∈ R. cos x = 0 при cos x > 0 для всех cos x < 0 для всех Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках: Наибольшее значение функции sin x = 1 в точках: Наименьшее значение функции sin x = −1 в точках:

---

Функция тангенс

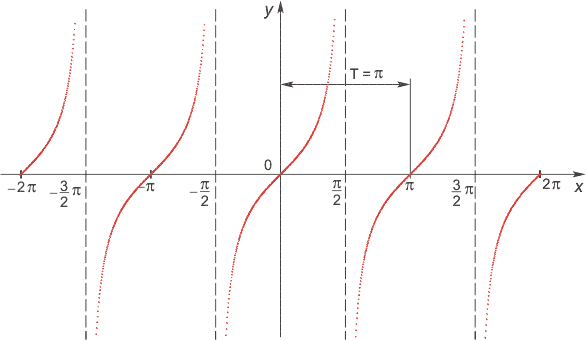Область определения функции — множество всех действительных чисел, кроме Множество значений функции — вся числовая прямая, т.е. тангенс — функция неограниченная. Функция нечетная: tg(−x)=−tg x для всех х из области определения. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения. tg x = 0 при tg x > 0 для всех tg x < 0 для всех Функция возрастает на промежутках:

---

Функция котангенс

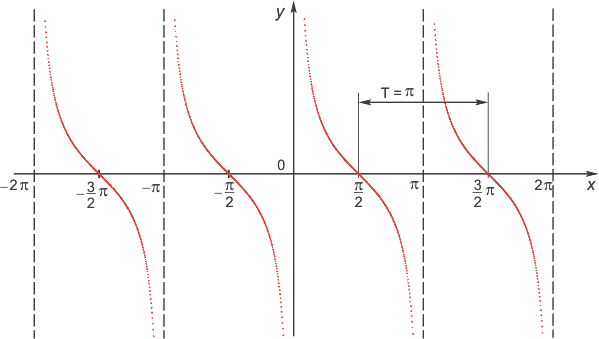Область определения функции — множество всех действительных чисел, кроме чисел Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная. Функция нечетная: ctg(−x)=−ctg x для всех х из области определения. График функции симметричен относительно оси OY.Функция периодическая с наименьшим положительным периодом π, т.е. ctg(x+π·k)=ctg x, k ∈ Z для всех х из области определения. ctg x = 0 при ctg x > 0 для всех ctg x < 0 для всех Функция убывает на каждом из промежутков