Степень с рациональным показателем, её свойства.
Выражение аn определено для всех а и n, кроме случая а=0 при n≤0. Напомним свойства таких степеней.
Для любых чисел а, b и любых целых чисел m и п справедливы равенства:
am*an=am+n;
am:аn=am-n (а≠0);
(аm)n = аmn;
(ab) n = an*bn;
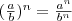 (b≠0);
(b≠0);
а1=а; а0=1 (а≠0).
Отметим также следующее свойство:
Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1.
В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа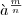 должна быть равна аm. Действительно, если свойство
должна быть равна аm. Действительно, если свойство
(ap)q=apq
выполняется, то
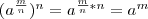
Последнее равенство означает (по определению корня n-й степени), что число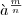 должно быть корнем п-й степени из числа аm.
должно быть корнем п-й степени из числа аm.
Определение.
Степенью числа а>0 с рациональным показателем r=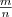 , где m — целое число, а n — натуральное (n > 1), называется число
, где m — целое число, а n — натуральное (n > 1), называется число 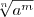
Итак, по определению
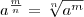 (1)
(1)
Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0.
Степень с иррациональным показателем.
Иррациональное число можно представить в виде предела последовательности рациональных чисел
можно представить в виде предела последовательности рациональных чисел  :
:  .
.
Зафиксируем положительное число а и поставим в соответствие каждому числу 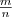 число
число 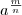 . Тем самым получим числовую функцию f(x) = ax, определенную на множестве Q рациональных чисел и обладающую ранее перечисленными свойствами. При а=1 функция f(x) = axпостоянна, так как 1x=1 для любого рационального х.
. Тем самым получим числовую функцию f(x) = ax, определенную на множестве Q рациональных чисел и обладающую ранее перечисленными свойствами. При а=1 функция f(x) = axпостоянна, так как 1x=1 для любого рационального х.
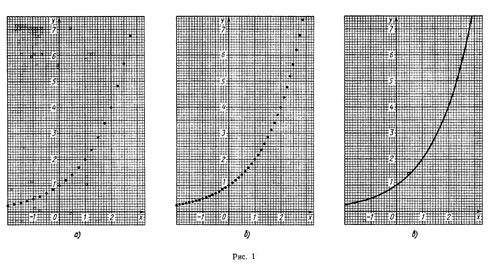
Нанесем несколько точек графика функции у =2x предварительно вычислив с помощью калькулятора значения 2x на отрезке [—2; 3] с шагом 1/4 (рис. 1, а), а затем с шагом 1/8 (рис. 1, б).Продолжая мысленно такие же построения с шагом 1/16, 1/32 и т. д., мы видим, что получающиеся точки можно соединить плавной кривой, которую естественно считать графиком некоторой функции, определенной и возрастающей уже на всей числовой прямой и принимающей значения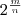 в рациональных точках
в рациональных точках 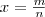 (рис. 1, в). Построив достаточно большое число точек графика функции
(рис. 1, в). Построив достаточно большое число точек графика функции 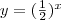 , можно убедиться в том, что аналогичными свойствами обладает и эта функция (отличие состоит в том, что функция
, можно убедиться в том, что аналогичными свойствами обладает и эта функция (отличие состоит в том, что функция 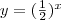 убывает на R).
убывает на R).
Эти наблюдения подсказывают, что можно так определить числа 2α и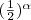 для каждого иррационального α, что функции , задаваемые формулами y=2x и
для каждого иррационального α, что функции , задаваемые формулами y=2x и 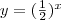 будут непрерывными, причем функция у=2x возрастает, а функция
будут непрерывными, причем функция у=2x возрастает, а функция 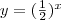 убывает на всей числовой прямой.
убывает на всей числовой прямой.
Опишем в общих чертах, как определяется число aα для иррациональных α при а>1. Мы хотим добиться того, чтобы функция у = ax была возрастающей. Тогда при любых рациональных r1 и r2, таких, что r1<α<r2, значение aα должно удовлетворять неравенствам ar1<аα<аr1.
Выбирая значения r1 и r2, приближающиеся к х, можно заметить, что и соответствующие значения ar1 и ar2 будут мало отличаться. Можно доказать, что существует, и притом только одно, число у, которое больше всех ar1 для всех рациональных r1и меньше всех ar2 для всех рациональных r2. Это число у по определению есть аα.
Например, вычислив с помощью калькулятора значения 2x в точках хn и х`n, где хn и х`n — десятичные приближения числа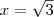 мы обнаружим, что, чем ближе хn и х`n к
мы обнаружим, что, чем ближе хn и х`n к 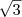 , тем меньше отличаются 2xn и 2x`n.
, тем меньше отличаются 2xn и 2x`n.
Так как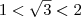 , то
, то
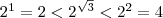
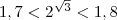 и, значит,
и, значит,
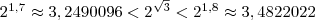
Аналогично, рассматривая следующие десятичные приближения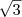 по недостатку и избытку, приходим к соотношениям
по недостатку и избытку, приходим к соотношениям
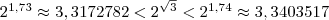 ;
;
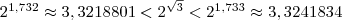 ;
;
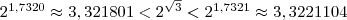 ;
;
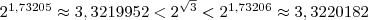 ;
;
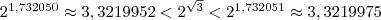 .
.
Значение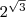 вычисленное на калькуляторе, таково:
вычисленное на калькуляторе, таково:
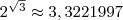 .
.
Аналогично определяется число aα для 0<α<1. Кроме того полагают 1α=1 для любого α и 0α=0 для α>0.
Показательная функция.

Выражение аn определено для всех а и n, кроме случая а=0 при n≤0. Напомним свойства таких степеней.
Для любых чисел а, b и любых целых чисел m и п справедливы равенства:
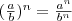 (b≠0);
(b≠0);Отметим также следующее свойство:
Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1.
В этом пункте мы обобщим понятие степени числа, придав смысл выражениям типа 20.3, 85/7, 4-1/2 и т. д. Естественно при этом дать определение так, чтобы степени с рациональными показателями обладали теми же свойствами (или хотя бы их частью), что и степени с целым показателем. Тогда, в частности, n-я степень числа
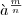 должна быть равна аm. Действительно, если свойство
должна быть равна аm. Действительно, если свойствовыполняется, то
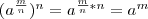
Последнее равенство означает (по определению корня n-й степени), что число
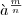 должно быть корнем п-й степени из числа аm.
должно быть корнем п-й степени из числа аm.Определение.
Степенью числа а>0 с рациональным показателем r=
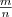 , где m — целое число, а n — натуральное (n > 1), называется число
, где m — целое число, а n — натуральное (n > 1), называется число 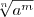
Итак, по определению
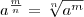 (1)
(1)Степень числа 0 определена только для положительных показателей; по определению 0r = 0 для любого r>0.
Степень с иррациональным показателем.
Иррациональное число
 можно представить в виде предела последовательности рациональных чисел
можно представить в виде предела последовательности рациональных чисел  :
:  .
.
Пусть  . Тогда существуют степени с рациональным показателем
. Тогда существуют степени с рациональным показателем  . Можно доказать, что последовательность этих степеней является сходящейся. Предел этой последовательности называется степенью с основанием
. Можно доказать, что последовательность этих степеней является сходящейся. Предел этой последовательности называется степенью с основанием  и иррациональным показателем
и иррациональным показателем  :
:  .
.
 . Тогда существуют степени с рациональным показателем
. Тогда существуют степени с рациональным показателем  . Можно доказать, что последовательность этих степеней является сходящейся. Предел этой последовательности называется степенью с основанием
. Можно доказать, что последовательность этих степеней является сходящейся. Предел этой последовательности называется степенью с основанием  и иррациональным показателем
и иррациональным показателем  :
:  .
.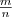 число
число 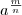 . Тем самым получим числовую функцию f(x) = ax, определенную на множестве Q рациональных чисел и обладающую ранее перечисленными свойствами. При а=1 функция f(x) = axпостоянна, так как 1x=1 для любого рационального х.
. Тем самым получим числовую функцию f(x) = ax, определенную на множестве Q рациональных чисел и обладающую ранее перечисленными свойствами. При а=1 функция f(x) = axпостоянна, так как 1x=1 для любого рационального х.
Нанесем несколько точек графика функции у =2x предварительно вычислив с помощью калькулятора значения 2x на отрезке [—2; 3] с шагом 1/4 (рис. 1, а), а затем с шагом 1/8 (рис. 1, б).Продолжая мысленно такие же построения с шагом 1/16, 1/32 и т. д., мы видим, что получающиеся точки можно соединить плавной кривой, которую естественно считать графиком некоторой функции, определенной и возрастающей уже на всей числовой прямой и принимающей значения
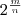 в рациональных точках
в рациональных точках 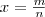 (рис. 1, в). Построив достаточно большое число точек графика функции
(рис. 1, в). Построив достаточно большое число точек графика функции 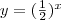 , можно убедиться в том, что аналогичными свойствами обладает и эта функция (отличие состоит в том, что функция
, можно убедиться в том, что аналогичными свойствами обладает и эта функция (отличие состоит в том, что функция 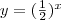 убывает на R).
убывает на R).Эти наблюдения подсказывают, что можно так определить числа 2α и
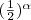 для каждого иррационального α, что функции , задаваемые формулами y=2x и
для каждого иррационального α, что функции , задаваемые формулами y=2x и 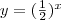 будут непрерывными, причем функция у=2x возрастает, а функция
будут непрерывными, причем функция у=2x возрастает, а функция 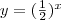 убывает на всей числовой прямой.
убывает на всей числовой прямой.Опишем в общих чертах, как определяется число aα для иррациональных α при а>1. Мы хотим добиться того, чтобы функция у = ax была возрастающей. Тогда при любых рациональных r1 и r2, таких, что r1<α<r2, значение aα должно удовлетворять неравенствам ar1<аα<аr1.
Выбирая значения r1 и r2, приближающиеся к х, можно заметить, что и соответствующие значения ar1 и ar2 будут мало отличаться. Можно доказать, что существует, и притом только одно, число у, которое больше всех ar1 для всех рациональных r1и меньше всех ar2 для всех рациональных r2. Это число у по определению есть аα.
Например, вычислив с помощью калькулятора значения 2x в точках хn и х`n, где хn и х`n — десятичные приближения числа
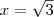 мы обнаружим, что, чем ближе хn и х`n к
мы обнаружим, что, чем ближе хn и х`n к 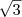 , тем меньше отличаются 2xn и 2x`n.
, тем меньше отличаются 2xn и 2x`n.Так как
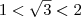 , то
, то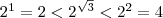
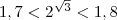 и, значит,
и, значит,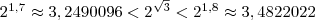
Аналогично, рассматривая следующие десятичные приближения
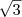 по недостатку и избытку, приходим к соотношениям
по недостатку и избытку, приходим к соотношениям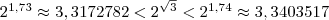 ;
;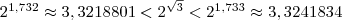 ;
;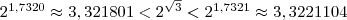 ;
;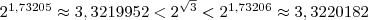 ;
;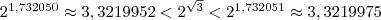 .
.Значение
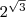 вычисленное на калькуляторе, таково:
вычисленное на калькуляторе, таково: 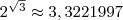 .
.Аналогично определяется число aα для 0<α<1. Кроме того полагают 1α=1 для любого α и 0α=0 для α>0.
Показательная функция.
При a > 0, a  =
=
 =
= 
Основные свойства показательной функции y = a x при a> 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток
(0;+ . )
) - Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1 < ax2 .
- При x = 0 значение функции равно 1.
- Если x > 0 , то a x > 1 и если x < 0, то 0 < a < 1.
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.
 |  |
Основные свойства показательной функции y = a x при 0 < a < 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток
(0;+ . )
) - Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1 > ax2 .
- При x = 0 значение функции равно 1.
- Если x > 0 , то 0 < a < 1 и если x < 0, то a x > 1. К общим свойствам показательной функции как при0 < a < 1, так и при a > 1 относятся:
- ax1 ax2 = ax1+ x2, для всех x1 и x2.
a−x=(ax)−1=1ax для любого x. nax=axn
nax=axn n . N
N n
n =1
=1 - (ab)x = ax bx для любых a, b > 0; a,b
 =1
=1 (ba)x=bxax для любых a, b > 0; a,b =1
=1 - ax1 = ax2, то x1 = x2.