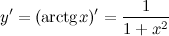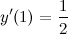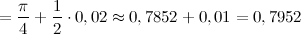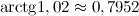Инвариантность формы дифференциала.
 ,
, ,
,
Применение дифференциала к приближённым вычислениям (Примеры).
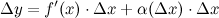
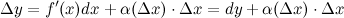
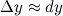
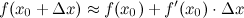
Формула дифференциала функции имеет вид
где  - дифференциал независимой переменной.
- дифференциал независимой переменной.
Пусть теперь дана сложная (дифференцируемая) функция  , где
, где  ,
,  . Тогда по формуле производной сложной функции находим
. Тогда по формуле производной сложной функции находим
так как  .
.
Итак,  , т.е. формула дифференциала имеет один и тот же вид для независимой переменной
, т.е. формула дифференциала имеет один и тот же вид для независимой переменной  и для промежуточного аргумента
и для промежуточного аргумента  , представляющего собой дифференцируемую функцию от
, представляющего собой дифференцируемую функцию от  .
.
Это свойство принято называть свойством инвариантности формулы или формы дифференциала. Заметим, что производная этим свойством не обладает.
Применение дифференциала к приближённым вычислениям (Примеры).
Приращение 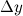 функции
функции  представимо в виде:
представимо в виде:
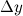 функции
функции  представимо в виде:
представимо в виде: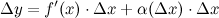
где функция 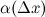 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента 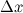 к нулю. Так как
к нулю. Так как 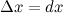 , то
, то
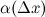 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента 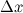 к нулю. Так как
к нулю. Так как 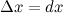 , то
, то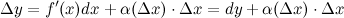
В силу того, что второе слагаемое 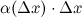 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому
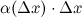 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому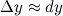
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:
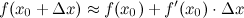
Пример
Задание.
|
С помощью дифференциала вычислить приближенно
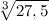 |
| Решение. |
Для вычисления данного значения применим формулу из теории
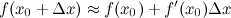
Введем в рассмотрение функцию
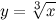 , а заданную величину представим в виде , а заданную величину представим в виде 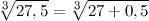 , тогда , тогда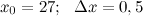
Вычислим
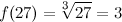 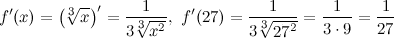
Подставляя все в формулу, окончательно получим
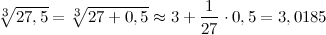 |
Ответ.
|  |
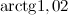 , заменяя приращение функции ее дифференциалом.
, заменяя приращение функции ее дифференциалом.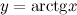 . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке 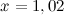 . Представим данное значение в виде следующей суммы:
. Представим данное значение в виде следующей суммы: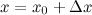
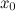 и
и 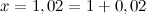 , то есть
, то есть 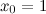 ,
, 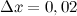 .
.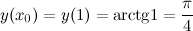
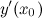 :
: