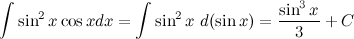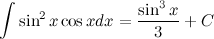Вычисления неопределенных интегралов: подведение под знак дифференциала.
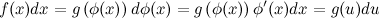
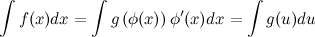
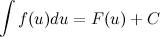
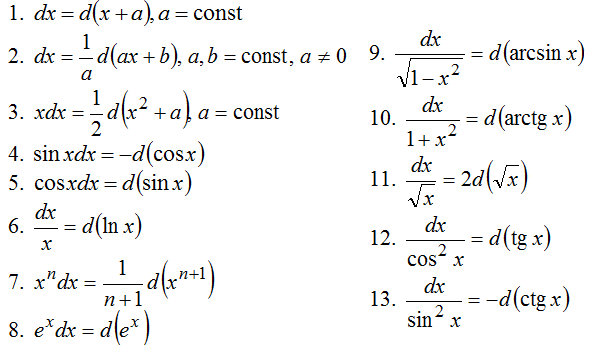
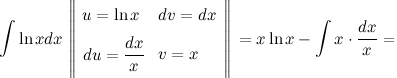
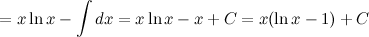
Пусть требуется найти неопределенный интеграл 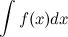 . Предположим, что существуют дифференцируемые функции
. Предположим, что существуют дифференцируемые функции 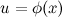 и
и 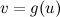 такие, что
такие, что
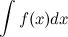 . Предположим, что существуют дифференцируемые функции
. Предположим, что существуют дифференцируемые функции 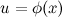 и
и 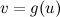 такие, что
такие, что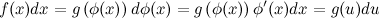
Тогда
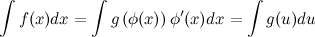
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.
Тогда, если 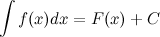 и
и 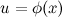 , то имеет место следующее равенство:
, то имеет место следующее равенство:
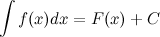 и
и 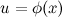 , то имеет место следующее равенство:
, то имеет место следующее равенство: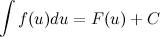
Замечание. При интегрировании методом подведения под знак дифференциала полезны следующие равенства для дифференциалов:
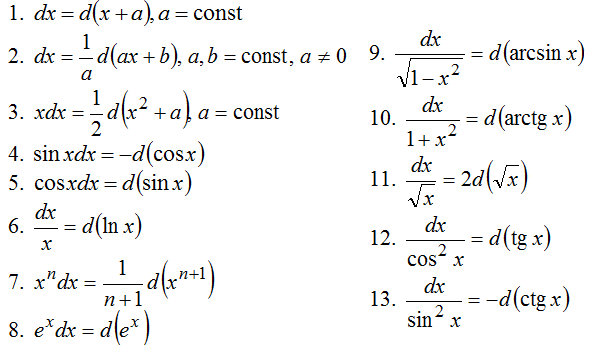
Примеры решения интегралов данным методом
Пример
Задание. Найти интеграл 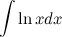
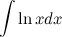
Решение. В исходном интеграле выделим функции  и
и  , затем выполним интегрирование по частям.
, затем выполним интегрирование по частям.
 и
и  , затем выполним интегрирование по частям.
, затем выполним интегрирование по частям.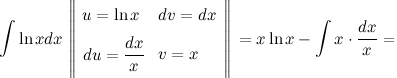
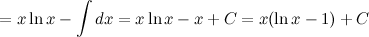
Ответ. 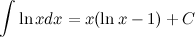
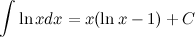
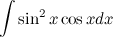
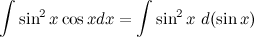
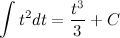 , то
, то