ФизМат: Определённый интеграл. Свойства определённого интеграла (линейность, аддитивность, теорема о среднем значении и другие).

Определённый интеграл.

Определенный интеграл — это аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых — интегрируемая функция или функционал, а вторая — область во множестве задания этой функции.
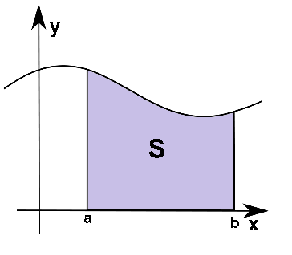
Проще говоря, это интеграл, численно равный площади части графика функции в пределах от a до b, т. е. площади криволинейной трапеции.

Определенный интеграл обозначается символом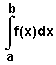

. Его можно найти по формуле Ньютона — Лейбница:
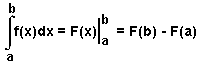
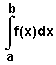определенный интеграл

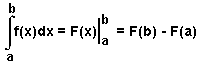
Свойства определённого интеграла (линейность, аддитивность, теорема о среднем значении и другие).

а) Если существует $\int\limits_{a}^{b}f(x)\,dx$ и $\lambda$ — любое число, то $\int\limits_{a}^{b}\lambda f(x)\,dx= \lambda\int\limits_{a}^{b}f(x)\,dx$ .

Доказательство. Из соответствующего свойства неопределенных интегралов следует, что если $F(x)$ — первообразная для $f(x)$ , то $\lambda F(x)$ — первообразная для $\lambda f(x)$ . Значит,

$\int\limits_{a}^{b}\lambda f(x)\,dx=\Bigl.{\lambda F(x)}\Bigr|_{a}^{b}= \lambda F(b)-\lambda F(a)=\lambda \Bigl(F(b)-F(a)\Bigr)= \lambda \int\limits_{a}^{b}f(x)\,dx\,.$

б) Если функции $y=f_1(x)$ и $y=f_2(x)$ имеют первообразные на отрезке $[a;b]$ , то

$\int\limits_{a}^{b}\Bigl(f_1(x)+f_2(x)\Bigr)dx= \int\limits_{a}^{b}f_1(x)\,dx+ \int\limits_{a}^{b}f_2(x)\,dx\,.$

Доказательство. Из соответствующего свойства неопределенных интегралов следует, что если $F_1(x)$ — первообразная для $f_1(x)$ , a $F_2(x)$ — первообразная для $f_2(x)$ на отрезке $[a;b]$ , то $F_1(x)+F_2(x)$ — первообразная для $f_1(x)+f_2(x)$ . Значит,

$\begin{aligned}\int\limits_{a}^{b}\Bigl(f_1(x)+f_2(x)\Bigr)dx&= \left.{\Bigl(F_1(x)+ F_2(x)\Bigr)}\right|_{a}^{b}= \Bigl(F_1(b)+F_2(b)\Bigr)-\Bigl(F_1(a)+F_2(a)\Bigr)=\\[-8pt] &=\Bigl(F_1(b)-F_1(a)\Bigr)+\Bigl(F_2(b)-F_2(a)\Bigr) =\int\limits_{a}^{b}f_1(x)\,dx+ \int\limits_{a}^{b} f_2(x)\,dx\,.\end{aligned}$

в) Если функция $f(x)$ имеет первообразную на отрезке $[a;b]$ и если $a<c<b$ , то (аддитивное свойство определенного интеграла)

$\int\limits_{a}^{b}f(x)\,dx= \int\limits_{a}^{c}f(x)\,dx+ \int\limits_{c}^{b} f(x)\,dx\,.$

Доказательство. Пусть $F(x)$ — первообразная для $f(x)$ . Тогда

$\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a),~~ \int\limits_{a}^{c}f(x)\,dx=F(c)-F(a),~~ \int\limits_{c}^{b}f(x)\,dx=F(b)-F(c).$

Аддитивность площади криволинейной трапеции

Но $F(b)-F(a)=\bigl(F(c)-F(a)\bigr)+\bigl(F(b)-F(c)\bigr)$ . Значит,

$\int\limits_{a}^{b}f(x)\,dx= \int\limits_{a}^{c}f(x)\,dx+ \int\limits_{c}^{b} f(x)\,dx\,,$

что и требовалось доказать.

Доказанное свойство имеет простой геометрический смысл: оно выражает аддитивность площади криволинейной трапеции. Так, на рисунке 5

$S_{aABb}= \int\limits_{a}^{b}f(x)\,dx;\quad S_1=\int\limits_{a}^{c}f(x)\,dx;\quad S_2=\int\limits_{c}^{b}f(x)\,dx$ . Тогда $s_{aABb}=S_1+S_2$ .

г) Если функция $y=f(x)$ имеет первообразную на отрезке $[a;b]$ , то справедливо равенство

$\int\limits_{a}^{b}f(x)\,dx= -\int\limits_{b}^{a}f(x)\,dx\,.$

Доказательство. Пусть $F(x)$ — первообразная для $f(x)$ . Тогда

$\int\limits_{a}^{b}f(x)\,dx=F(b)-F(a),\qquad \int\limits_{b}^{a}f(x)\,dx=F(a)-F(b).$

Но $F(b)-F(a)=-\bigl(F(a)-F(b)\bigr)$ , откуда и следует доказываемое утверждение.

д) $\int\limits_{a}^{a}f(x)\,dx=0$ . Доказательство: $\int\limits_{a}^{a}f(x)\,dx=F(a)-F(a)=0$ .

Пример 7. Вычислить интеграл от рациональной дроби: $\int\limits_{0}^{3} \frac{x^4}{x^2+1}\,dx$ .

Решение. Сначала выделим целую часть неправильной дроби, содержащейся под знаком интеграла:

$\int\limits_{0}^{3} \frac{x^4}{x^2+1}\,dx= \int\limits_{0}^{3} \frac{(x^4-1)+1}{x^2+1}\,dx= \int\limits_{0}^{3} \frac{(x^2-1)(x^2+1)+1}{x^2+1}\,dx= \int\limits_{0}^{3} \!\left(x^2-1+\frac{1}{x^2+1}\right)\!dx\,.$

Воспользовавшись теперь свойством б) определенного интеграла, получим:

$\begin{aligned}\int\limits_{0}^{3} \!\left(x^2-1+\frac{1}{x^2+1}\right)\!dx&= \int\limits_{0}^{3}x^2\,dx-\int\limits_{0}^{3}dx+\int\limits_{0}^{3}\frac{dx}{x^2+1}= \left.{\frac{x^3}{3}}\right|_{0}^{3}- \Bigl.{x}\Bigr|_{0}^{3}+ \Bigl.{\operatorname{arctg}x}\Bigr|_{0}^{3}=\\ &=(9-0)-(3-0)+ (\operatorname{arctg}3- \operatorname{arctg}0)= 6+\operatorname{arctg}3.\end{aligned}$

понедельник, 9 декабря 2013 г.

Определённый интеграл. Свойства определённого интеграла (линейность, аддитивность, теорема о среднем значении и другие).

понедельник, 9 декабря 2013 г.