Векторное, параметрическое, «в отрезках» и нормальное уравнения плоскости.
Уравнение плоскости в отрезках
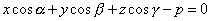 , (1)
, (1)
Уравнение плоскости, проходящей через три точки
М0(x0, y0, z0), М1(x1, y1, z1) и М2(x2, y2, z2), не лежащие на одной прямой, имеет вид

Параметрическое уравнение.Так же, как для прямой, условие (5.3.1) может быть переписано в виде
или, в координатной форме, в системе координат Oxyz
 (5.3.4)
(5.3.4)
Уравнения (5.3.3), (5.3.4) называются параметрическими уравнениями плоскости в векторной и координатной формах.
Расстояние от точки до плоскости (с доказательством).
Доказательство. Расстояние от точки  до плоскости
до плоскости  -- это, по определению, длина перпендикуляра
-- это, по определению, длина перпендикуляра  , опущенного из точки
, опущенного из точки  на плоскость
на плоскость  (рис. 11.9).
(рис. 11.9).
 Рис.11.9.Расстояние от точки до плоскости
Рис.11.9.Расстояние от точки до плоскости
 Откуда
Откуда
Точка  лежит на плоскости
лежит на плоскости  , поэтому ее координаты удовлетворяют уравнению плоскости:
, поэтому ее координаты удовлетворяют уравнению плоскости:  . Отсюда находим, что
. Отсюда находим, что  . Подставив полученный результат в формулу (11.9), получим
. Подставив полученный результат в формулу (11.9), получим  . Так как
. Так как  , то из формулы (11.8) следует формула (11.7).
, то из формулы (11.8) следует формула (11.7).
Уравнение плоскости в отрезках
Если плоскость пересекает оси OX, OY и OZ в точках с координатами (
a
, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках
x
| + |
y
| + |
z
| = 1 |
a
|
b
|
c
|
Нормальным уравнением плоскости называется ее уравнение, написанное в виде
где 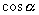 ,
, 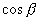 ,
, 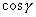 - направляющие косинусы нормали плоскоти, p - расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).
- направляющие косинусы нормали плоскоти, p - расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).
Уравнение плоскости, проходящей через три точки
М0(x0, y0, z0), М1(x1, y1, z1) и М2(x2, y2, z2), не лежащие на одной прямой, имеет вид

Параметрическое уравнение.Так же, как для прямой, условие (5.3.1) может быть переписано в виде
r = r0 + up1 + v2, u, v ∈ R, (5.3.3)
или, в координатной форме, в системе координат Oxyz
 (5.3.4)
(5.3.4)Уравнения (5.3.3), (5.3.4) называются параметрическими уравнениями плоскости в векторной и координатной формах.
Расстояние от точки до плоскости (с доказательством).
Предложение 11.1 Пусть плоскость  задана уравнением
задана уравнением  и дана точка
и дана точка  . Тогда расстояние
. Тогда расстояние  от точки
от точки  до плоскости
до плоскости  определяется по формуле
определяется по формуле

Вектор  и нормальный вектор n плоскости
и нормальный вектор n плоскости  параллельны, то есть угол
параллельны, то есть угол  между ними равен 0 или
между ними равен 0 или  , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому
, если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому
Координаты точки  , которые нам неизвестны, обозначим
, которые нам неизвестны, обозначим  . Тогда
. Тогда  . Так как
. Так как  , то
, то  . Раскрыв скобки и перегруппировав слагаемые, получим
. Раскрыв скобки и перегруппировав слагаемые, получим

