Векторное, параметрическое, «в отрезках» и нормальное уравнения прямой на плоскости.
Общее уравнение
Уравнение прямой в отрезках
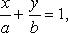
Нормальное уравнение прямой (рис. 4.11)
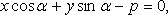
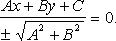
Расстояние от точки до прямой (с доказательством)
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
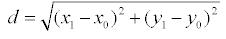 (1)
(1)
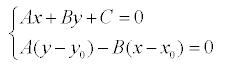
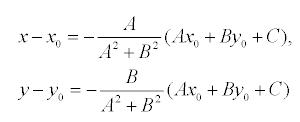
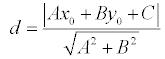
Общее уравнение
Ax + By + C (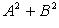 > 0).
> 0).
Вектор 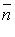 = (А; В) - нормальный вектор прямой.
= (А; В) - нормальный вектор прямой.
В векторном виде: 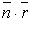 + С = 0, где
+ С = 0, где 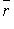 - радиус-вектор произвольной точки на прямой (рис. 4.11).
- радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 - прямая параллельна оси Ox;
2) Ax + C = 0 - прямая параллельна оси Oy;
3) Ax + By = 0 - прямая проходит через начало координат;
4) y = 0 - ось Ox;
5) x = 0 - ось Oy.
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x
=
l t
+
x
0 | |
y
=
m t
+
y
0 |
где (
x
0,
y
0) - координаты точки лежащей на прямой,
{l
,
m}
- координаты направляющего вектора прямой.Уравнение прямой в отрезках
где a, b - величины отрезков, отсекаемых прямой на осях координат.
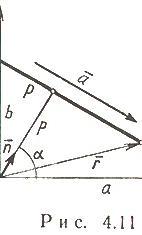
Нормальное уравнение прямой (рис. 4.11)
где 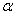 - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Здесь 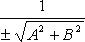 - нормируемый множитель прямой; знак выбирается противоположным знаку C, если
- нормируемый множитель прямой; знак выбирается противоположным знаку C, если 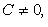 и произвольно, если C = 0.
и произвольно, если C = 0.
Расстояние от точки до прямой (с доказательством)
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если задано уравнение прямой A
x
+ B
y
+ C = 0, то расстояние от точки M(M
x
, M
y
) до прямой можно найти, используя следующую формулу
d
= | |A·M
x
+ B·M
y
+ C| |
| (A2 + B2)1/2 |
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
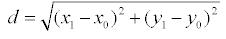 (1)
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
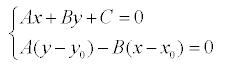
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
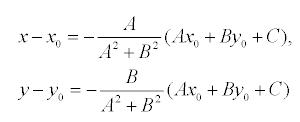
Подставляя эти выражения в уравнение (1), находим:
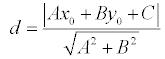
Теорема доказана.