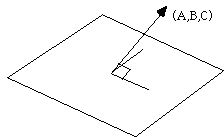
Плоскость. Линейность уравнения плоскости и обратное утверждение. Нормальный вектор.

Плоскость. 

Пло́скость — это поверхность, образованная кинематическим движением образующей по направляющей, представляющей из себя прямую 

Линейность уравнения плоскости и обратное утверждение. 

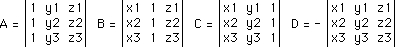
Стандартное уравнение плоскости - Ax + By + Cz + D = 0 Вектор (A, B, C) перпендикулярен плоскости. Уравнение плоскости по трем точкам (x1,y1,z1), (x2,y2,z2), (x3,y3,z3) можно получить из следующих опрееделителей: Раскрывая, получаем A = y1 (z2 - z3) + y2 (z3 - z1) + y3 (z1 - z2)  B = z1 (x2 - x3) + z2 (x3 - x1) + z3 (x1 - x2)  C = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)  - D = x1 (y2 z3 - y3 z2) + x2 (y3 z1 - y1 z3) + x3 (y1 z2 - y2 z1) Следует заметить, что, если все точки лежат на одной прямой, то (A,B,C) будет (0,0,0). Знак s = Ax + By + Cz + D определяет, с какой стороны по отношению к плоскости находится точка (x,y,z). Если s > 0, то точка лежит в той стороне, куда указывает нормальный вектор (A,B,C). Если s < 0 - на противаположной стороне, а в случае s = 0 точка принадлежит плоскости.

Нормальный вектор.

Нормальный вектор плоскости - это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.