Вычисления неопределенных интегралов: интегрирование по частям.
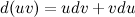
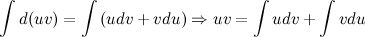
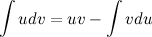
Рассмотрим функции 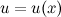 и
и 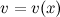 , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
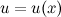 и
и 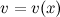 , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство: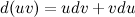
Проинтегрировав левую и правую части последнего равенства, получим:
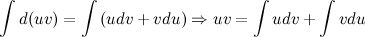
Полученное равенство перепишем в виде:
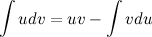
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл 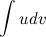 можно свести к нахождению интеграла
можно свести к нахождению интеграла 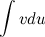 , который может быть более простым.
, который может быть более простым.
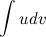 можно свести к нахождению интеграла
можно свести к нахождению интеграла 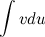 , который может быть более простым.
, который может быть более простым.
Замечание
Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
1) 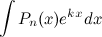 ;
; 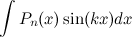 ;
; 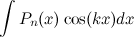
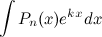 ;
; 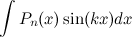 ;
; 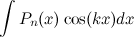
Здесь 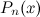 - многочлен степени
- многочлен степени 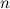 ,
, 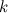 - некоторая константа. В данном случае в качестве функции
- некоторая константа. В данном случае в качестве функции  берется многочлен, а в качестве
берется многочлен, а в качестве 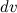 - оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется
- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется 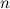 раз.
раз.
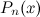 - многочлен степени
- многочлен степени 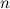 ,
, 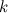 - некоторая константа. В данном случае в качестве функции
- некоторая константа. В данном случае в качестве функции  берется многочлен, а в качестве
берется многочлен, а в качестве 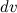 - оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется
- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется 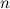 раз.
раз.Примеры решения интегралов данным методом
Пример
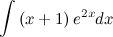
 , затем выполним интегрирование по частям.
, затем выполним интегрирование по частям.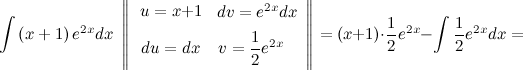
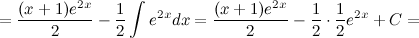
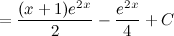
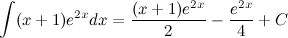
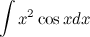
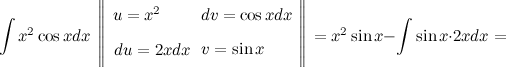
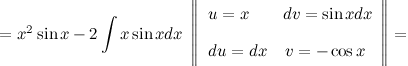
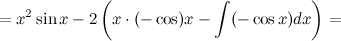
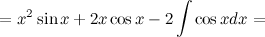
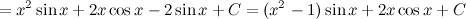
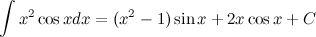
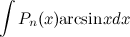 ;
; 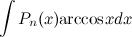 ;
; 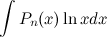
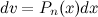 , а в качестве
, а в качестве