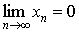Массивы 10.2

Ввести массив из N натуральных чисел. Найти в нем и вывести на печать монотонно возрастающую подпоследовательность максимальной длины.

uses crt;
const nmax=20;
var a:array[1..nmax] of integer;
n,i,j,k,mx,imx:byte;

begin
clrscr;
repeat
write('Размер массива до ',nmax,' n=');
readln(n);
until n in [1..nmax];
writeln('Введите элементы массива, в том числе возрастающие участки:');
for i:=1 to n do
begin
write('a[',i,']=');
readln(a[i]);
end;
clrscr;
writeln('Массив:');
for i:=1 to n do
write(a[i],' ');
writeln;
writeln;
i:=2;mx:=0;imx:=0;
while i<=n do
if a[i]>a[i-1] then
begin
j:=i;k:=1;
while (a[j]>a[j-1])and(j<=n) do
begin
j:=j+1;
k:=k+1;
end;
if k>mx then
begin
mx:=k;
imx:=i-1;
end;
i:=i+k;
end
else i:=i+1;
if mx=0 then write('Нет участков возрастания!')
else
begin
writeln('Максимальная последовательность возрастающих чисел=',mx);
for i:=imx to imx+mx-1 do
write(a[i],' ');
end;
readln
end.

Массивы 10.1

Дан массив целых чисел найти

Максимальный элемент массива и его порядковый номер
Элемент наиболее близкий к среднему арифметическому всех элементов массива

var A:array [1 .. 4 ] of integer;
k,max,s,i:integer;
s1:real;


function maxmas(var b,c:integer):boolean;
var k:integer;
begin


for k:=1 to 4 do begin
if b > c then maxmas:=true end;

end


begin
for k:=1 to 4 do begin
write('Введите А (',k,') ');
readln(A[ k ]); end;
max:=1;
for k:=2 to 4 do begin



if maxmas(A[k],A[max])=true then max:=k; end;

for i:=1 to 4 do begin
k:=i+1;
end;
for i:=1 to 4 do begin
s:=s+A[i];
end;
s1:=s/k;
if s1>A[i] then begin
writeln('среднее арифметическое = ',A[i]);
end;

begin
writeln('Максимальный элемент = ', A [ max ] );
writeln('Его порядковый номер = ', max);
end;
end.

Методом Монте-Карло

На отрезке [a, b] заданы функции f1(x) и f2(x). Вычислить площадь фигуры, закключенной между этими функциями методом Монте-Карло
A=0; B=Pi/2 ; f1(x)=cos(x); f2(x)= ось OX

var a,b,S,s1,h,x,y: real;
i,n: integer;

function f(x: real): real;
begin
f:=cos(x);
end;

begin
n:=100;
a:=0;
b:=PI/2;
randomize();
for i:=1 to n do
begin
x:=random()*b;
y:=random()*1;
if(f(x)>y)then
s:=s+1;
end;
s:=s/n*b;

while abs(s-s1)>0.01 do
begin
s1:=s;
n:=n*10;
randomize();
for i:=1 to n do
begin
x:=random()*b;
y:=random()*1;
if(f(x)>y)then
s:=s+1;
end;
s:=s/n*b;
end;

writeln(s, ' ', n);
readln;
end.

Метод трапеции

На отрезке [a, b] заданы функции f1(x) и f2(x). Вычислить площадь фигуры, закключенной между этими функциями методом трпеции

A=0; B=Pi/2 ; f1(x)=cos(x); f2(x)= ось OX


var a,b,S,h,int,int2: real;
i,n: integer;

function f(x: real): real;
begin
f:=cos(x);
end;

begin
n:=2;
a:=0;
b:=PI/2;

h:=(b-a)/n;
for i:=1 to n-1 do
S:=S+f(a + h*i);
int:=h*((f(a)+f(b))/2+S);

while abs(int-int2)>0.01 do
begin
n:=n*2;
s:=0;
int2:=int;
h:=(b-a)/n;
for i:=1 to n-1 do
S:=S+f(a + h*i);
int:=h*((f(a)+f(b))/2+S);
end;
writeln(int, ' ', n);
readln;
end.

13) Логарифмическая функция ее свойства и график.

Логарифмическая функция ее свойства и график.

12) Логарифм числа. Основное логарифмическое тождество. Докажите формулу переворачивания логарифма logab=1/logba и формулы перехода к новому основанию.

Докажите формулу переворачивания логарифма logab=1/logba и формулы перехода к новому основанию.

Вообщем телеофн придется перевернуть)))

11) Логарифм числа. Основное логарифмическое тождество. Докажите формулы вынесения показателя степени для логарифмического числа и для основания логарифма.

Докажите формулы вынесения показателя степени для логарифмического числа и для основания логарифма.

10) Логарифм числа. Основное логарифмическое тождество. Докажите формулы для логарифма произведения и логарифма частного.

Логарифм числа.

Логарифм положительного числа b по основанию a (a>0; a не равно 1) называется показатель степени  в которую нужно возвести a, чтобы получить b.

Основное логарифмическое тождество.

Докажите формулы для логарифма произведения и логарифма частного.

Основное логарифмическое тождество: 

9) Бесконечно убывающая геометрическая прогрессия, её сумма.

Бесконечно убывающая геометрическая прогрессия, её сумма.

Бесконечно убывающей геометрической прогрессией называется бесконечная геометрическая прогрессия, знаменатель которой удовлетворяет условию .

При неограниченном возрастании  сумма  первых  членов бесконечно убывающей геометрической прогрессии стремится к числу , которое называется суммой бесконечно убывающей геометрической прогрессии.

Вывести формулу сумм членов бесконечно убывающей геометрической прогрессии.

8) Второй замечательный предел (с доказательством).

Второй замечательный предел (с доказательством).

ПРИМЕРЫ

ЗАДАЧА 427 Вычислите предел lim(x

Вычислите предел lim(x→∞)(3x+13/x−5)^4x+7 Смотреть решение...

ЗАДАЧА 428 Найти предел lim(x

Найти предел lim(x→1)(7−6x)^(x/(3x−3)). Смотреть решение...

ЗАДАЧА 429 Вычислить предел lim(x

Вычислить предел lim(x→+∞) x(ln(x+1)−lnx) Смотреть решение...

7) Теорема о "зажатой" последовательности. Достаточное условие сходимости числовой последовательности.

Теорема о "зажатой" последовательности.

Пусть заданы {Xn}, {Yn}, {Zn}, причем Xn<=Yn<=Zn для всех n принадлежащих N и lim Xn = lim Zn = a, тогда lim Yn = a

Если даны три последовательности a_n, b_n и c_n причём lim a_n=lim c_n=b и для всх n выполняется неравенство a_n <= b_{n <=} c_n то и последовательность b_n тоже имеет предел, равный b.

Достаточное условие сходимости числовой последовательности.

Теорема 13. Если монотонная последовательность  ограничена, то она сходится.

Доказательство. Так как последовательность  ограничена, то множество ее элементов имеет точные верхнюю  и нижнюю  грани. Пусть  – неубывающая последовательность и – точная верхняя грань множества ее элементов. Это означает, что для любого числа  можно указать такой элемент , что  и . Эти два неравенства равносильны неравенству  или . Так как  – неубывающая последовательность, то при  выполняется  или . Это означает, что при  выполняется  или . Таким образом, . Аналогично доказывается случай, когда  – невозрастающая последовательность.

6) Бесконечно большая последовательность, её связь с бесконечно малой. Предельный переход в неравенствах.

Бесконечно большая последовательность, её связь с бесконечно малой.

  Определение. Последовательность { хn} называется бесконечно большой, если для как угодно большого любого положительного числа А существует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | xn | > A:

Теорема 1. Если последовательность а_n является бесконечно большой, то последовательность 1/a_n является бесконечно малой.

Предельный переход в неравенствах.

Если для всех значений N, кроме, может быть, конечного числа, выполняется неравенство a_n<b_n, при этом пределы этих последовательностей равны a и b соответственно, то a<b.

Тут

5) Арифметическая теорема о пределах.

Арифметическая теорема о пределах.


Теорема. Сумма (разность) двух сходящихся последовательностей есть сходящаяся последовательность предел которой равен сумме (разности) Xn и Yn




Теорема. Произведение сходящихся последовательностей Xn и Yn есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей Xn и Yn

Теорема. Частное двух сходящихся последовательностей Xn и Yn, при условие, что предел последовательности Yn не равен, есть сходящаяся последовательность, предел которой равен частному Xn и Yn

4) Бесконечно малая последовательность. Теорема о последовательности, её пределе и бесконечно малой последовательности. Теорема о произведении ограниченной и бесконечно малой последовательностей.

Бесконечно малая последовательность.

Последовательность {xn} называется бесконечно малой, если

для

Теорема о последовательности, её пределе и бесконечно малой последовательности.

Для того что бы число а являлось пределом последовательности a_n необходимо и достаточно чтобы последовательность {a_n-a} была бесконечно малой.

Теорема о произведении ограниченной и бесконечно малой последовательностей.

Произведение ограниченной и бесконечно малой последовательностей, так же является бесконечно малой последовательностью.

3) Предел числовой последовательности, геометрическая интерпретация, теорема о единственности предела. Необходимое условие сходимости (ограниченность).

Предел числовой последовательности, геометрическая интерпретация, теорема о единственности предела.



Пример:

ЗАДАЧА 391 Вычислить предел числовой

Вычислить предел числовой последовательности Смотреть решение...

Геометрическая интерпретация

Начиная с некоторого члена все последующие члены последовательности попадают в окрестности точки a с радиусом E

Теорема о единственности предела

Определение: Последовательность может иметь только один предел.

Доказательство: Предположим противное, т.е. пусть последовательность {x_n} такая, что

lim_n→∞xn=a  и lim_n→∞xn=b  и a <> b.

Тогда поскольку число a – предел последовательности, то должно выполняться неравенство:

| x_n - a| < ε        и             | x_n - b| < ε

Очевидно, что между двумя неравными числами (a <> b) находится бесконечно много других чисел. Поэтому всегда можно выбрать такое число ε > 0, что ε-окрестность точки a не будет пересекаться с ε-окрестностью точки b.

                (a – ε, a + ε)   (b – ε,  b + ε )  = (пустое_множество)

Поскольку число a является пределом последовательности {x_n}, то начиная с некоторого номера n > N все члены этой последовательности попадут в ε-окрестность точки a , а вне этой окрестности может оказаться только конечное число членов: x₁, x₂…x_n. Но тогда в ε-окрестность точки b может попасть только что-то из чисел x₁, x₂…x_n и не больше, а это противоречит тому, что число b предел {x_n} (Если b– предел, то в ε-окрестность точки b должно попадать не меньше, чем в ε-окрестность точки a). Следовательно, предположение о том, что a<> b не верно. Из этого следует, что a = b, а значит, предел единственен. Что и требовалось доказать.

Необходимое условие сходимости (ограниченность).

Теорема. Если последовательность имеет предел то она ограничена.

Док-во:

Пусть lim an =a, E=1, тогда вне окрестности (a-1;a+1) находится конечное число элементов a1, a1...an

m = min{a1,...ak; a-1}
M = max{a1..ak; a+1}

m<=an<=M для всех n из N, значит последовательность {an} - ограничена

Замечание. Сходимость означает ограниченность, но ограниченность не означает сходимость.